软件评测师笔记(2)计算机组成结构
1. 计算机系统硬件基本组成
计算机的硬件系统基本由五大部分组成:运算器,控制器,存储器,输入设备,输出设备
CPU由运算器,控制器,寄存器和内部总线组成
CUP中最主要的部分是运算器和控制器
CPU的功能:实现程序控制,操作控制,时序控制,数据处理功能
运算器由算术逻辑单元ALU,累加寄存器AC,状态条件寄存器PSW,数据缓冲器DR组成
- 算术逻辑单元ALU:实现对数据的算术和逻辑运算
- 累加寄存器AC:运算结果或源操作数的存放区
- 状态条件寄存器PSW:保存指令运行结果的条件码内容,如溢出标志等
- 数据缓冲器DR:暂时存放内存的指令或数据
运算器功能:执行所有算术运算,执行所有逻辑运算并进行逻辑测试(如与,或,非)
控制器由指令寄存器IR,程序计数器PC,地址寄存器AR,指令译码器ID等组成
- 指令寄存器IR:暂存CPU执行指令,存放当前正在执行的指令,对用户是完全透明的
- 程序计数器PC:存放下一条执行的指令的地址
- 地址寄存器AR:保存当前CPU所访问的内存地址
- 指令译码器ID:分析指令操作码
控制器功能:控制整个CPU的工作,最为重要,包括程序控制,时序控制等
存储器分为内部存储器和外部存储器
- 内部存储器:即内存,容量小,速度快,临时存放数据
- 外部存储器:即硬盘,容量大,速度慢,长期保存数据
输入设备和输出设备统称为外部设备,即外设
2. 计算机体系结构分类
Flynn分类法分为4种类型:
单指令流单数据流(Single Instruction Single Data,SISD)
多指令流单数据流(Multiple Instruction Single Data,MISD)
单指令流多数据流(Single Instruction Multiple Data,SIMD)
多指令流多数据流(Multiple Instruction Multiple Data,MIMD)

3. 指令寻址方式
指令寻址方式
- 顺序寻址方式:当执行一段程序时,是一条指令接着一条指令地顺序执行
- 跳跃寻址方式:指下一条指令的地址码不是由程序计数器给出,而是由本条指令直接给出。程序跳跃后,按新的指令地址开始顺序执行。因此,程序计数器的内容也必须相应改变,以便及时跟踪新的指令地址
指令操作数的寻址方式
- 立即寻址方式:指令的地址码字段指出操作数本身
- 直接寻址方式:在指令的地址字段中直接指出操作数在主存中的地址
- 隐含寻址方式:在指令的地址不是明显给出的,而是隐含在指令中
- 寄存器寻址方式:指令地址码字段所指向的存储单元中存的是操作数
- 间接寻址方式:指令地址码字段所指向的存储单元中存的是操作数的地址
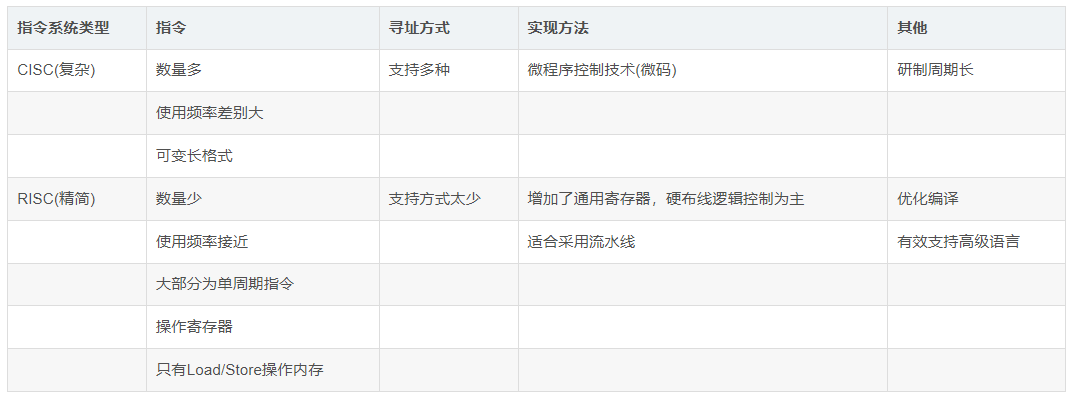
4. CISC和RISC指令系统
CISC是复杂指令系统,兼容性强,指令繁多、长度可变,由微程序实现;
RISC是精简指令系统,指令少,使用频率接近,主要依靠硬件实现(通用寄存器、硬布线逻辑控制)。
5. 指令流水线
将指令分成不同段,每段由不同的部分去处理,因此可以产生叠加的效果,所有的部件去处理指令的不同段,如下图所示
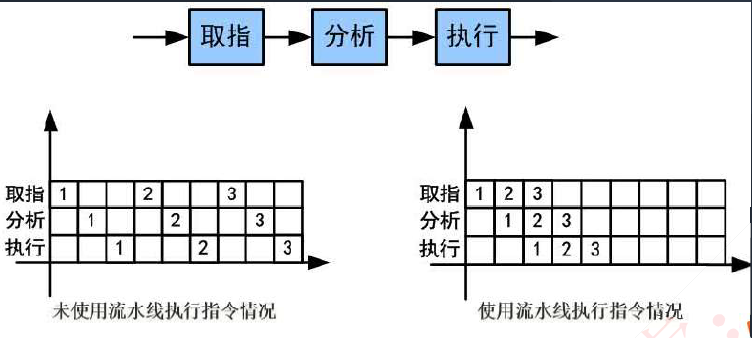
- 流水线周期:指令分成不同执行段,其中执行时间最长的段为流水线周期
- 流水线执行时间:1条指令总执行时间+(总指令条数-1)*流水线周期
- 流水线吞吐量:总指令条数/流水线执行时间
- 流水线加速比:不使用流水线总执行时间/使用流水线总执行时间
6. 存储系统
计算机采用分级存储体系的目的主要是为了解决存储容量、成本和速度之间的矛盾问题
- 两级存储:Cache-主存,主存-辅存(虚拟存储体系)
存储器分类
访问方式可分为
- 按地址访问的存储器
- 按内容访问的存储器:相联存储器,把数据或数据一部分作为关键字
寻址方式可分为
- 随机存储器(RAM):可对任何存储单元存入或读取数据,访问任何一个存储单元所需时间是相同的
- 顺序存储器(SAM):访问数据所需时间与数据所在存储位置相关,磁带是典型的顺序存储器
- 直接存储器(DAM):介于RAM和SAM之间,磁盘是一种直接存储器,它对磁道的寻址是随机的,而在一个磁道内,则是顺序寻址
在CPU工作时,送出的是主存单元的地址,而应从Cache存储器中读/写信息。这就需要将主存地址转换为Cache存储器地址,这种地址的转换称为地址映射,由硬件自动完成映射,有三种映射方式:
- 直接映射:将Cache存储器等分成块,主存也等分成块并编号,主存中的块与Cache中的块对应关系是固定的,也即两者块号相同才能命中。地址变换简单但不灵活,容易造成资源浪费
- 全相联映射:同样等分成块并编号。主存中任意一块都与Cache中任意一块对应。因此可以随意调入Cache任意位置,但地址变换复杂,速度较慢。因为主存可以随意调入Cache任意块,只有当Cache满了才会发生块冲突,是最不容易发生冲突的映射方式
- 组组相连映射:前面两种方式的结合,将Cache存储器先分块再分组,主存也同样先分块再分组,组间采用直接映射,即主存中组号与Cache中组号相同的组才能命中,但组内全相联映射,即组号相同的两个组内的所有块可以任意调换
7. 输入输出技术
计算机和外设间的数据交互方式:
- 程序控制(查询)方式:CPU主动查询外设是否完成数据传输,效率极低。
- 程序中断方式:外设完成数据传输后,向CPU发送中断,等待CPU处理数据,效率相对较高。中断响应时间指的是从发出中断请求到开始进入中断处理程序;中断处理时间指的是从中断处理开始到中断处理结束。中断向量提供中断服务程序的入口地址。多级中断嵌套,使用堆栈来保护断点和现场。
- DMA方式(直接主存存取):CPU只需完成必要的初始化等操作,数据传输的整个过程都由DMA控制器来完成,在主存和外设之间建立直接的数据通路,效率很高。
- 在一个总线周期结束后,CPU会响应DMA请求开始读取数据;CPU响应程序中断方式请求是在一条指令执行结束时。
8. 总线结构
从广义上讲,任何链接两个以上的电子元器件的导线都可以称之为总线,通常分为以下三类
- 内部总线:内部芯片级别的总线,芯片与处理器之间通信的总线
- 系统总线:是板级总线,用于计算机内部各个部分之间的链接,具体分为
- 数据总线:并行数据传输位数。数据总线宽度等于系统位数
- 地址总线:系统可管理的内存空间大小。存储容量 = 等于 2^n Byte(其中n为地址总线宽度)
- 控制总线:传送控制命令
- 外部总线:设备一级的总线,微机和外部设备的总线
某DRAM芯片的存储容量为512K*16位,则芯片的地址和数据线宽度分别为?
解:
1. 芯片为16位,因此数据线宽度为16
2. 芯片的存储容量位512K,512K = (2^9 * 2^10)Byte = 2^19Byte,因此地址总线宽度为19
9. 系统可靠性分析
- 平均无故障时间:MTTF=1/失效率
- 平均故障修复时间:MTTR=1/修复率
- 平均故障间隔时间:MTBF=MTTF+MTTR
- 系统可用性=MTTF/MTBF*100%
可靠性可以用可以用MTTF/ (1+MTTF)来度量
假设每个设备的可靠性为R1 R2 R3,则不同系统的可靠性R计算公式如下
- 串联系统:R1 * R2 * R3
- 并联系统:1 - (1-R1) * (1-R2) * (1-R3)
10. 进制转化
10.1 R进制向十进制转化
将R进制数的每一位数值用 R^k 形式表示,其中k与该位和小数点之间的距离有关。
当该位位于小数点左边,k值是该位和小数点之间数码的个数。
当该位位于小数点右边,k值是负值,其绝对值是该位和小数点之间数码的个数加1。
即小数点左侧k从0开始,小数点右侧k从-1开始
### 二进制 ###
10100.01 = 1*2^4 + 1*2^2 + 1*2^-2
### 七进制 ###
604.01 = 6*7^2 + 4*7^0 + 1*7^-2
10.2 十进制向R进制转化
我们使用短除法进行转换
结果由下往上写

10.3 二进制转八进制或十六进制
八进制:将二进制数由后向前每三位划分一组,分别计算每组的十进制值,最后组合得到的值便为转换后的八进制的值
十六进制:将二进制数由后向前每四位划分一组,分别计算每组的十进制值,最后组合得到的值便为转换后的十六进制的值
11. 数的表示
- 机器数:各种数值在计算机中表示的形式,其特点是使用二进制技术制,数的符号用0和1表示,小数点则隐含不占位置。机器数有无符号数和带符号数之分。无符号数表示正数,没有符号位。带符号数最高位为符号位,正数符号位为0,负数符号位为1
- 浮点数:表示方法为N=F*2^E,其中E称为阶码,F称为尾数。阶码为带符号的纯整数。尾数为带符号的纯小数。二进制如101.011=0.101011*2^3。数值范围由阶码确定,数值精度由尾数确定
12. 原码,反码,补码,移码
带符号数有下列编码方式,当真值为-45时:
原码:一个数的正常二进制表示,最高位表示符号,数值0的源码有两种形式:+0(00000000)和-0(10000000)。45对应原码为10101101
反码:正数的反码即原码;负数的反码是在原码的基础上,除符号位外,其他各位按位取反。数值0的反码也有两种形式:+0(00000000),-0(1 1111111)。-45对应反码为11010010
补码:正数的补码即原码;负数的补码是在原码的基础上,除符号位外,其他各位按位取反,而后末位+1,若有进位侧产生进位。因此数值0的补码只有一种形式+0=-0=00000000。-45对应补码为11010011
移码:用作浮点运算的阶码,无论正数负数,都是将该原码的补码的首位(符号位)取反得到移码。-45对应移码为01010011
机器字长为时各种码制表示的带符号数的取值范围(差别在于0的表示,原码和反码分+0和-0,补码只有一个0,因此可以多表示一个。):

⚠️ 计算机中大多数情况下会用补码进行运算。 原码,反码和移码在计算过程中结果可能不符合预期,例如1+(-1)
13. 校验码
13.1 奇偶校验码
在编码中增加1位校验码来使编码中1的个数位奇数(奇校验)或者偶数(偶校验)从而使码距变为2。
- 奇校验:编码中含有奇数个1发送给接收方,接收方收到后会计算收到的编码中有多少个1,如果是奇数个则无误
- 偶校验:同理,只是编码中有偶数个1
假设现在有一段编码
10010
我们要使用奇校验,我们需要在编码最后增加1位,并且保证加1位之后的编码中有奇数个1
此时我们得到的编码是:100101
而当我使用偶校验,我们同样需要在编码最后增加1位,并且保证加1位之后的编码中有偶数个1
此时我们得到的编码是:100100
从上述可以看出,奇偶校验只能检1位错,且无法纠错
⚠️ 码距:就单个编码A:00而言,其码距为1,因为其只需要改变一位就变成了另一个编码。在两个编码中,从A码到B码的转换所需要改变的位数称为码距,如A:00要转换为B:11,码距为2。一般来说码距越大越利于纠错和检错。
13.2 循环冗余校验码CRC
CRC只能检错,不能纠错。
其原理是找出一个能整除多项式的编码,因此首先要将原报文除以多项式,将所得的余数作为校验位加在原始报文之后,将整体作为发送数据发送给接收方。
⚠️ 模2运算其实是将两数进行异或
原始报文为11001010101,其生成多项式为x^4+x^3+x+1。对其进行CRC编码后的结果为?
解:
首先我们需要对多项式进行置换,将多项式从0次幂开始到最高次幂,若当前次幂存在则为1,不存在则为0
x^4+x^3+x+1 则置换为 11011
第二步我们要在原始报文后面加上多项式位数个0暂时充当校验位作为被除数
此时的被除数为110010101010000
将被除数和置换后的多项式进行模2除法
得出一个四位余数:0011,将做为校验位
我们发送出去的数据为原报文+校验位:110010101010011
接收方将收到的数据110010101010011与多项式置换后的11011进行摸2运算,若余数为0说明校验正确,数据传输正常
-------------------------------------------------------------------------------------------------
110010101010000与11011进行模2运算
110010101010000
11011
---------------
10010
11011
---------------
10011
11011
---------------
10000
11011
---------------
10111
11011
---------------
11000
11011
---------------
11000
11011
---------------
0011
13.3 海明校验码
本质上也是利用奇偶性来检错和纠错的检验方法,构成方法是在数据位之间的确定的位置上(2^k位)插入k个校验位,通过扩大码距实现检错和纠错。
设数据位是n位,校验码是k位,则n和k必须满足 2^k-1≥n+k
求信息1011的海明码
解:
首先我们要明确校验位和数据位之间的关系,校验码存在于第2^k位,且保证2^k-1>=n+k,如下表
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 位数
|I4 |I3 |I2 | |I1 | | | 信息位
| | | |r2 | |r1 |r0 | 校验位
换成当前题目数据为
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 位数
| 1 | 0 | 1 | | 1 | | | 信息位
| | | |r2 | |r1 |r0 | 校验位
接下来进行校验位的计算
首先我们需要确定每一位校验码到底校验那些信息位,将信息位(位数)拆分成二进制表示
- 7=4+2+1, 由第4位的校验位(r2),第2位的校验位(r1)和第1位的校验位(r0)共同校验
- 6=4+2,由第4位的校验位(r2)和第2位的校验位(r1)共同校验
- 5=4+1, 由第4位的校验位(r2)和第1位的校验位(r0)共同校验
- 3=2+1,由第2位的校验位(r1)和第1位的校验位(r0)共同校验
此时我们可以知道第4位的校验位校验第7,6,5位的数据,因此第4位的校验位r2等于7,6,5这三个位置数据的值进行异或运算的结果
- r2 = 1,0,1进行异或 = 0
同理我们可以得出
- r1 = 0
- r0 = 1
如下表所示
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 位数
| 1 | 0 | 1 | | 1 | | | 信息位
| | | | 0 | | 0 | 1 | 校验位
最终我们得到的海明吗为:1010101
海明码的检错和纠错原理如下:
检错
- 接收方收到海明码之后,会将每一位校验位的值与其校验的位数的值分别异或,即做如下三组运算 r2 ⊕ I4 ⊕ I3 ⊕ I2 ,r1 ⊕ I4 ⊕ I3 ⊕ I1, r0 ⊕ I4 ⊕ I2 ⊕ I1,如果是偶校验,那么运算得到的结果应全为0表明传输正确,如果是奇校验得到的结果应全为1表明传输正确
- 以偶校验举例。我们在得到海明码时,校验位的值是通过其校验的位数的值异或得来的,即做了如下三组运算 I4 ⊕ I3 ⊕ I2,I4 ⊕ I3 ⊕ I1,I4 ⊕ I2 ⊕ I1(我们接下来称这三组运算的结果为A1,A2,A3)。因此当传输过程无误时,校验位的值必定等于其对应运算方法的结果,即 r2=A1 r1=A2 r0=A3。所以两值再次异或之后结果为0证明传输前后数据一致
纠错
- 假设接收到的数据中第四位出错,此时三组运算 r2 ⊕ I4 ⊕ I3 ⊕ I2,r1 ⊕ I4 ⊕ I3 ⊕ I1,r0 ⊕ I4 ⊕ I2 ⊕ I1 的结果为 1, 0, 0
- 证明r2中验证的某一位有问题,此时我们按照r2r1r0(高位到低位)的顺序将结果排列成2进制的值 100 转换为十进制为4,即第4位出错了
- 纠错方法便是将出错的值取非